29. Game of Life

According to Wikipedia's article: "The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970."

The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):

1. Any live cell with fewer than two live neighbors dies as if caused by under-population.

2. Any live cell with two or three live neighbors lives on to the next generation.

3. Any live cell with more than three live neighbors dies, as if by over-population.

4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.

The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the m x n grid board, return the next state.

Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cell

Example 1:

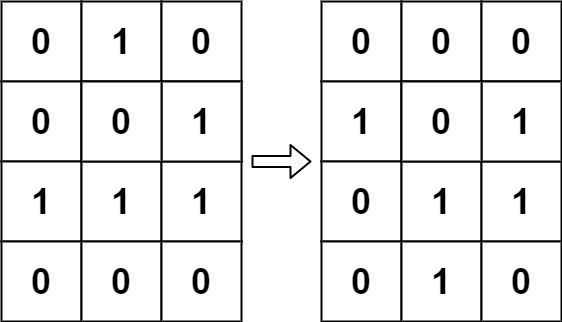
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

Example 2:

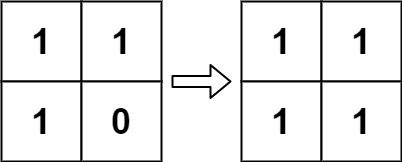
Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]

Solution: (Using a copy of vector)

class Solution
{
public:
    void gameOfLife(vector<vector<int>> &board)
    {

        int n = board.size();
        int m = board[0].size();

        vector<vector<int>> v = board;

        for (int i = 0; i < n; i++)
        {
           
            for (int j = 0; j < m; j++)
            {
                int dir1 = (i - 1 >= 0) ? v[i - 1][j] : -1;
                int dir2 = (i + 1 < n) ? v[i + 1][j] : -1;
                int dir3 = (j - 1 >= 0) ? v[i][j - 1] : -1;
                int dir4 = (j + 1 < m) ? v[i][j + 1] : -1;
                int dir5 = (i - 1 >= 0 && j - 1 >= 0) ? v[i - 1][j - 1] : -1;
                int dir6 = (i + 1 < n && j + 1 < m) ? v[i + 1][j + 1] : -1;
                int dir7 = (i - 1 >= 0 && j + 1 < m) ? v[i - 1][j + 1] : -1;
                int dir8 = (i + 1 < n && j - 1 >= 0) ? v[i + 1][j - 1] : -1;
                int s = 0;
                
                if (dir1 != -1)
                {
                    s += dir1;
                }
                if (dir2 != -1)
                {
                    s += dir2;
                }
                if (dir3 != -1)
                {
                    s += dir3;
                }
                if (dir4 != -1)
                {
                    s += dir4;
                }
                if (dir5 != -1)
                {
                    s += dir5;
                }
                if (dir6 != -1)
                {
                    s += dir6;
                }
                if (dir7 != -1)
                {
                    s += dir7;
                }
                if (dir8 != -1)
                {
                    s += dir8;
                }

                if (v[i][j] == 1)
                {
                    if (s < 2 || s > 3)
                    {
                        board[i][j] = 0;
                    }
                    else if (s == 2 || s == 3)
                    {
                        board[i][j] = 1;
                    }
                }

                if (v[i][j] == 0)
                {
                    if (s == 3)
                    {
                        board[i][j] = 1;
                    }
                }
            }
        }
    }
};

Time Complexity: O(n * m) Space Complexity: O(n * m)

Solution: (Using Constant Space)

Approach: The cell which changes from 0 - 1 has no effect on results so we mark it as 2. The cell which changes from 1 to 0 has effect so we mark it as -1 so that the abs becomes 1

class Solution
{
public:
    void gameOfLife(vector<vector<int>> &board)
    {

        int n = board.size();
        int m = board[0].size();

        vector<int> dir{0, 1, -1};

        for (int i = 0; i < n; i++)
        {

            for (int j = 0; j < m; j++)
            {
                int count = 0;
                for (int d1 = 0; d1 < 3; d1++)
                {
                    for (int d2 = 0; d2 < 3; d2++)
                    {
                        if (d1 == 0 && d2 == 0)
                        {
                            continue;
                        }

                        int row = i + dir[d1];
                        int col = j + dir[d2];
                        if (row >= 0 && col >= 0 && row < n && col < m)
                        {
                            if (abs(board[row][col]) == 1)
                            {
                                count++;
                            }
                        }
                    }
                }

                if (board[i][j] == 1)
                {
                    if (count < 2 || count > 3)
                    {
                        board[i][j] = -1;
                    }
                }

                if (board[i][j] == 0)
                {
                    if (count == 3)
                    {
                        board[i][j] = 2;
                    }
                }
            }
        }

        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {

                if (board[i][j] == -1)
                {
                    board[i][j] = 0;
                }

                if (board[i][j] == 2)
                {
                    board[i][j] = 1;
                }
            }
        }
    }
};

Time Complexity: O(n * m) Space Complexity: O(1)