2.Lowest Common Ancestor of a Binary Tree

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

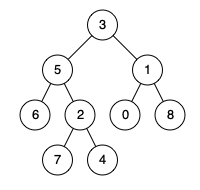
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [1,2], p = 1, q = 2
Output: 1

Lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).

Solution I

Method 1 (By Storing root to n1 and root to n2 paths): 1) Find path from root to n1 and store it in a vector or array. 2) Find path from root to n2 and store it in another vector or array. 3) Traverse both paths till the values in arrays are same. Return the common element just before the mismatch.

class Solution
{
public:
    bool findPath(TreeNode *root, TreeNode *p, vector<TreeNode *> &v)
    {
        if (root == NULL)
        {
            return false;
        }

        v.push_back(root);

        if (root == p)
        {
            return true;
        }

      
        if (findPath(root->left, p, v))
        {
            return true;
        }
        
      
        if (findPath(root->right, p, v))
        {
            return true;
        }
        
        v.pop_back();
        return false;
    }

    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
    {
        vector<TreeNode *> v1;
        vector<TreeNode *> v2;
        TreeNode *res = NULL;

        findPath(root, p, v1);
        findPath(root, q, v2);
        
        int i;
        int x = min(v1.size(),v2.size());
        for (i = 0; i < x; i++)
        {
            if (v1[i] != v2[i])
            {
                break;
            }
        }
        res = v1[i - 1];
        return res;
    }
};

Time Complexity O(n), and extra space of O(n) The tree is traversed twice, and then path arrays are compared.

Solution II

Method 2 (Using Single Traversal)

class Solution
{
public:
    TreeNode *findLCA(TreeNode *root, TreeNode *p, TreeNode *q)
    {

        if (root == NULL)
        {
            return NULL;
        }

        if (root == p || root == q)
        {
            return root;
        }

        TreeNode *lt = findLCA(root->left, p, q);
        TreeNode *rt = findLCA(root->right, p, q);

        if (lt and rt)
        {
            return root;
        }

        if (lt)
        {
            return lt;
        }

        if (rt)
        {
            return rt;
        }

        return NULL;
    }

    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
    {

        TreeNode *t = findLCA(root, p, q);
        return t;
    }
};

Time Complexity: O(n) , Const space used.