12. All Paths From Source to Target

Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1, and return them in any order.

The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

Example 1:

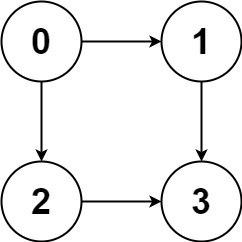
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

Example 2:

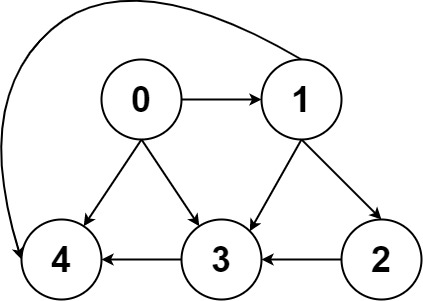
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

Example 3:
Input: graph = [[1],[]]
Output: [[0,1]]

Example 4:
Input: graph = [[1,2,3],[2],[3],[]]
Output: [[0,1,2,3],[0,2,3],[0,3]]


Example 5:
Input: graph = [[1,3],[2],[3],[]]
Output: [[0,1,2,3],[0,3]]

Solution: (DFS)

class Solution
{
public:
    void dfs(vector<vector<int>> graph, int src, int dest, vector<int> v, vector<vector<int>> &res)
    {

        if (src == dest)
        {
            v.push_back(src);
            res.push_back(v);
            return;
        }

        v.push_back(src);
        for (int i = 0; i < graph[src].size(); i++)
        {
            dfs(graph, graph[src][i], dest, v, res);
        }

        return;
    }

    vector<vector<int>> allPathsSourceTarget(vector<vector<int>> &graph)
    {

        vector<int> v;
        vector<vector<int>> res;
        int n = graph.size();
        dfs(graph, 0, n - 1, v, res);
        return res;
    }
};

Optimized some space by reusing the vector:

class Solution
{
public:
    void dfs(vector<vector<int>> graph, int src, int dest, vector<int> &v, vector<vector<int>> &res)
    {

        if (src == dest)
        {
            v.push_back(src);
            res.push_back(v);
            v.pop_back();
            return;
        }

        v.push_back(src);
        for (int i = 0; i < graph[src].size(); i++)
        {
            dfs(graph, graph[src][i], dest, v, res);
        }
        v.pop_back();

        return;
    }

    vector<vector<int>> allPathsSourceTarget(vector<vector<int>> &graph)
    {

        vector<int> v;
        vector<vector<int>> res;
        int n = graph.size();
        dfs(graph, 0, n - 1, v, res);
        return res;
    }
};

Time Complexity: O(v^v)