Deadlock in Operating System
1. Deadlock
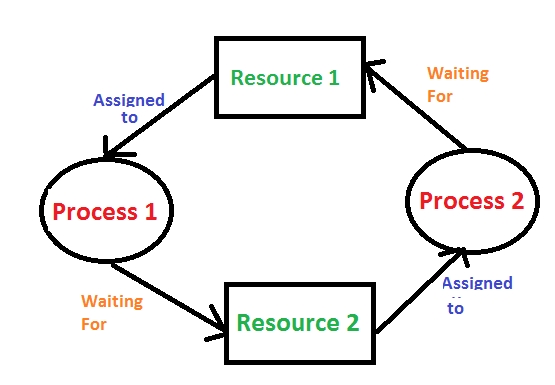
Deadlock is a situation where a set of processes are blocked because each process is holding a resource and waiting for another resource acquired by some other process.
2. Conditions for deadlock
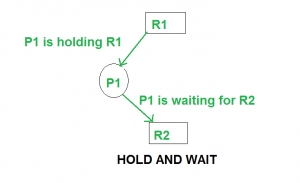
Deadlock can arise if the following four conditions hold simultaneously (Necessary Conditions) Mutual Exclusion: One or more than one resource are non-shareable (Only one process can use at a time) Hold and Wait: A process is holding at least one resource and waiting for resources. No Preemption: A resource cannot be taken from a process unless the process releases the resource. Circular Wait: A set of processes are waiting for each other in circular form.
3. Methods for handling deadlock
There are three ways to handle deadlock 1) Deadlock prevention or avoidance: The idea is to not let the system into a deadlock state. One can zoom into each category individually, Prevention is done by negating one of above mentioned necessary conditions for deadlock. Avoidance is kind of futuristic in nature. By using strategy of “Avoidance”, we have to make an assumption. We need to ensure that all information about resources which process will need are known to us prior to execution of the process. We use Banker’s algorithm (Which is in-turn a gift from Dijkstra) in order to avoid deadlock.
2) Deadlock detection and recovery: Let deadlock occur, then do preemption to handle it once occurred.
3) Ignore the problem altogether: If deadlock is very rare, then let it happen and reboot the system. This is the approach that both Windows and UNIX take.
4. Deadlock Prevention And Avoidance
Deadlock Prevention:
Deadlock Prevention: Deadlock Characteristics
Mutual Exclusion
Hold and Wait
No preemption
Circular wait
We can prevent Deadlock by eliminating any of the above four conditions.
Eliminate Mutual Exclusion It is not possible to dis-satisfy the mutual exclusion because some resources, such as the tape drive and printer, are inherently non-shareable.
Eliminate Hold and wait
Allocate all required resources to the process before the start of its execution, this way hold and wait condition is eliminated but it will lead to low device utilization. for example, if a process requires printer at a later time and we have allocated printer before the start of its execution printer will remain blocked till it has completed its execution.
The process will make a new request for resources after releasing the current set of resources. This solution may lead to starvation.
Eliminate No Preemption Preempt resources from the process when resources required by other high priority processes.
Eliminate Circular Wait Each resource will be assigned with a numerical number. A process can request the resources increasing/decreasing. order of numbering. For Example, if P1 process is allocated R5 resources, now next time if P1 ask for R4, R3 lesser than R5 such request will not be granted, only request for resources more than R5 will be granted.
Deadlock Avoidance:
Deadlock Avoidance:Deadlock avoidance can be done with Banker’s Algorithm and Resource allocation graph
Banker’s Algorithm Bankers’s Algorithm is resource allocation and deadlock avoidance algorithm which test all the request made by processes for resources, it checks for the safe state, if after granting request system remains in the safe state it allows the request and if there is no safe state it doesn’t allow the request made by the process.
Inputs to Banker’s Algorithm:
Max need of resources by each process.
Currently, allocated resources by each process.
Max free available resources in the system.
The request will only be granted under the below condition:
If the request made by the process is less than equal to max need to that process.
If the request made by the process is less than equal to the freely available resource in the system.
Example:
Note: Deadlock prevention is more strict than Deadlock Avoidance.
5. Deadlock Recovery
There are two approaches of breaking a Deadlock:
1. Process Termination: To eliminate the deadlock, we can simply kill one or more processes. For this, we use two methods:
(a) Abort all the Deadlocked Processes: Aborting all the processes will certainly break the deadlock, but with a great expense. The deadlocked processes may have computed for a long time and the result of those partial computations must be discarded and there is a probability to recalculate them later.
(b) Abort one process at a time until deadlock is eliminated: Abort one deadlocked process at a time, until deadlock cycle is eliminated from the system. Due to this method, there may be considerable overhead, because after aborting each process, we have to run deadlock detection algorithm to check whether any processes are still deadlocked.
2. Resource Preemption: To eliminate deadlocks using resource preemption, we preempt some resources from processes and give those resources to other processes. This method will raise three issues –
(a) Selecting a victim: We must determine which resources and which processes are to be preempted and also the order to minimize the cost.
(b) Rollback: We must determine what should be done with the process from which resources are preempted. One simple idea is total rollback. That means abort the process and restart it.
(c) Starvation: In a system, it may happen that same process is always picked as a victim. As a result, that process will never complete its designated task. This situation is called Starvation and must be avoided. One solution is that a process must be picked as a victim only a finite number of times.
Last updated
Was this helpful?