23. Minimum Time to Collect All Apples in a Tree

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

Example 1:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

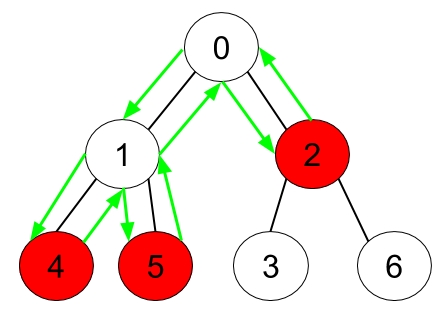
Example 2:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

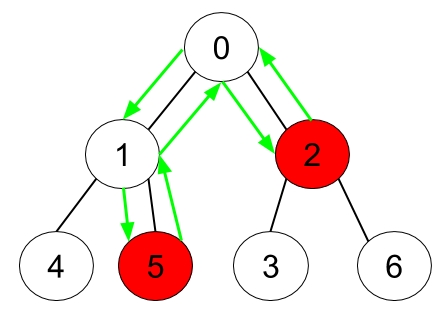
Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

Solution: (DFS)

class Solution
{
public:
    int dfs(vector<int> v[], int node, vector<bool> hasApple, vector<bool> &vs)
    {
        vs[node] = true;
        int x = 0;
        for (int i = 0; i < v[node].size(); i++)
        {
            if (!vs[v[node][i]])
            {
                x += dfs(v, v[node][i], hasApple, vs);
            }
        }

        if (hasApple[node] || x != 0)
        {
            x = x + 2;
        }

        return x;
    }

    int minTime(int n, vector<vector<int>> &edges, vector<bool> &hasApple)
    {

        vector<int> v[n];
        vector<bool> vs(n);

        for (int i = 0; i < edges.size(); i++)
        {
            v[edges[i][0]].push_back(edges[i][1]);
            v[edges[i][1]].push_back(edges[i][0]);
        }

        int sum = dfs(v, 0, hasApple, vs);
        if (sum != 0)
        {
            return sum - 2;
        }
        return sum;
    }
};

Time Complexity: O(V + E)