21. Critical Connections in a Network

Finding the Bridges

An edge is a bridge removing it increases the number of components in a graph If there are no backedge from a node to its parent or ancestor then the edge is a bridge.

There are n servers numbered from 0 to n - 1 connected by undirected server-to-server connections forming a network where connections[i] = [ai, bi] represents a connection between servers ai and bi. Any server can reach other servers directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some servers unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

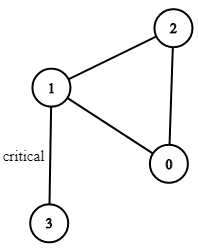
Solution:

Tarjan's algorithm

class Solution
{
public:
    vector<vector<int>> res;
    int time = 0;
    
    void findBridges(vector<int> v[], vector<int> &disc, vector<int> &low, vector<int> &parent, int src)
    {

        disc[src] = time;
        low[src] = time;
        time++;

        for (int i = 0; i < v[src].size(); i++)
        {
            int node = v[src][i];
            
            if (disc[node] == -1)
            {
                parent[node] = src;
                findBridges(v, disc, low, parent, node);
                low[src] = min(low[src], low[node]);
           
                if (low[node] > disc[src])
                {
                    res.push_back({node, src});
                }
            }
            else if (parent[src] != node)
            {
                low[src] = min(low[src], low[node]);
            }
        }

        return;
    }

    vector<vector<int>> criticalConnections(int n, vector<vector<int>> &connections)
    {

        vector<int> v[n];

        for (int i = 0; i < connections.size(); i++)
        {
            int a = connections[i][0];
            int b = connections[i][1];

            v[a].push_back(b);
            v[b].push_back(a);
        }

        vector<int> disc(n, -1);
        vector<int> low(n, -1);
        vector<int> parent(n, -1);

        findBridges(v, disc, low, parent, 0);

        return res;
    }
};

Time Complexity: O(V + E)