17. Binary Tree Maximum Path Sum

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any path.

Example 1:

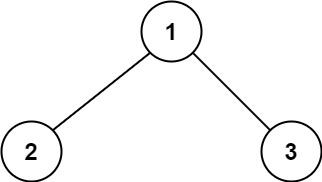
Input: root = [1,2,3]
Output: 6
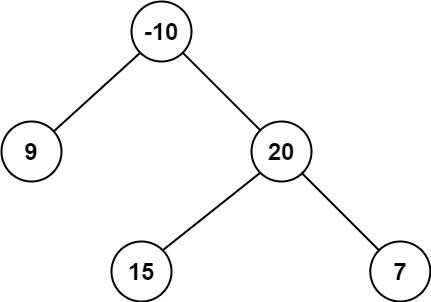
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6

Example 2:

Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42

Solution: (Using Postorder)

Approach:

There are 3 cases: 1. The current node is in the path of the max sum / the current node is starting of max sum 2. The current node is the root of max sum 3. The current node is not included in max sum we return to upper nodes only the value of max sum if node is in path.As returning other two are not necessary

class Solution
{
public:
    int findMaxSum(TreeNode *node, int &res)
    {

        if (node == NULL)
        {
            return 0;
        }

        int leftSum = findMaxSum(node->left, res);
        int rightSum = findMaxSum(node->right, res);

        int max_straight = max(max(leftSum, rightSum) + node->val, node->val); //case-1
        int max_root = max(leftSum + rightSum + node->val, max_straight);      //case-2
        res = max(res, max_root);

        return max_straight;
    }

    int maxPathSum(TreeNode *root)
    {

        int max_val = INT_MIN;
        int res = findMaxSum(root, max_val);
        return max_val;
    }
};