37. Count Square Submatrices with All Ones

Given a m * n matrix of ones and zeros, return how many square submatrices have all ones.

Example 1:

Input: matrix =
[
  [0,1,1,1],
  [1,1,1,1],
  [0,1,1,1]
]
Output: 15
Explanation: 
There are 10 squares of side 1.
There are 4 squares of side 2.
There is  1 square of side 3.
Total number of squares = 10 + 4 + 1 = 15.

Example 2:

Input: matrix = 
[
  [1,0,1],
  [1,1,0],
  [1,1,0]
]
Output: 7
Explanation: 
There are 6 squares of side 1.  
There is 1 square of side 2. 
Total number of squares = 6 + 1 = 7.

Approach

The idea is to scan each cell in the matrix to update the placeholder result variable with the number of squares that can be formed from the currently looking cell (when it is the bottom right corner cell of the any possible square).

image

image

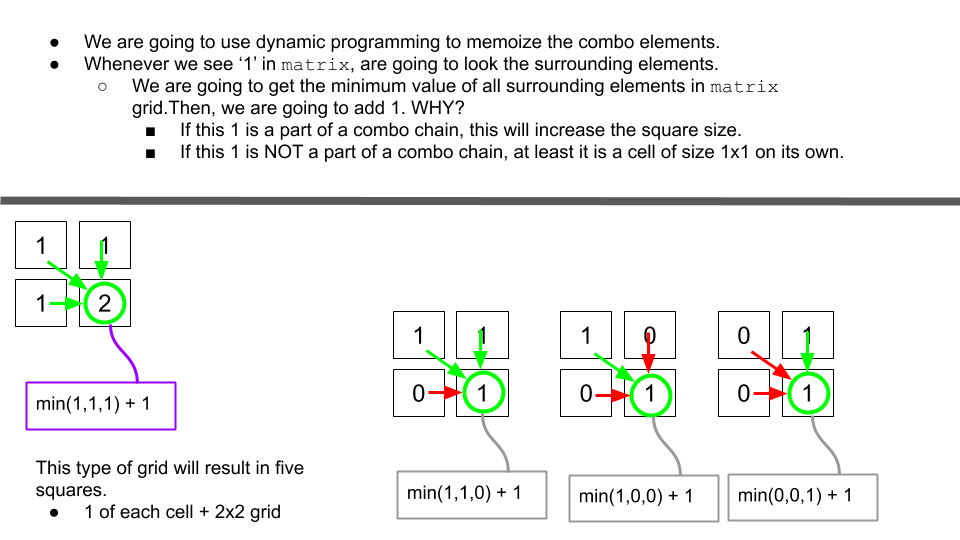
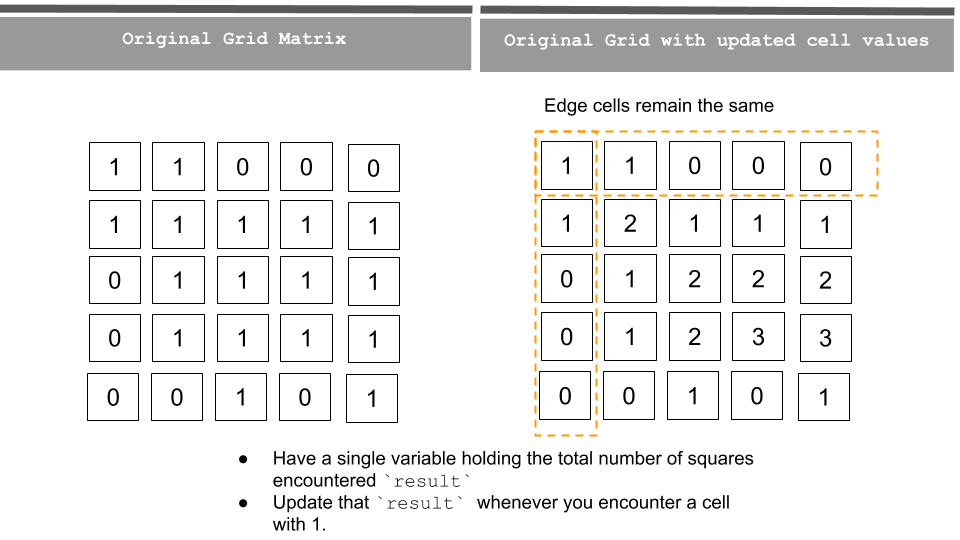
Solution: (Dp)

class Solution
{
public:
    int countSquares(vector<vector<int>> &matrix)
    {

        int n = matrix.size();
        int m = matrix[0].size();

        for (int i = 0; i < n; i++)
        {

            for (int j = 0; j < m; j++)
            {

                if (i == 0 || j == 0 || matrix[i][j] == 0)
                {
                    continue;
                }

                matrix[i][j] = min(matrix[i - 1][j - 1], min(matrix[i - 1][j], matrix[i][j - 1])) + 1;
            }
        }

        int s = 0;
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {
                s += matrix[i][j];
            }
        }

        return s;
    }
};

Time Complexity: O(n * m)