Memory Management
Degree of Multiprogramming
The degree of multiprogramming describes the maximum number of processes that a single-processor system can accommodate efficiently.
Why Use Memory Management
This technique helps in placing the programs in memory in such a way so that memory is utilized to its fullest extent.
It allows you to check how much memory needs to be allocated to processes.
Increase the Degree of multiprogramming
Memory Allocation Techniques
Contiguous Memory Allocation:- In contiguous memory allocation, a process can be stored only in a contiguous fashion.
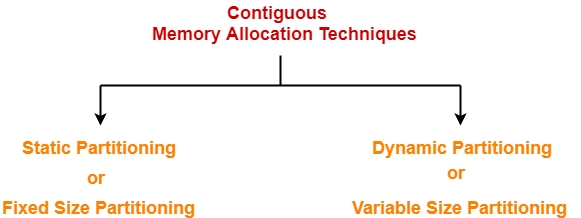
1. Fixed (or static) Partitioning
This is the oldest and simplest technique used to put more than one process in the main memory. In this partitioning, the number of partitions (non-overlapping) in RAM is fixed but the size of each partition may or may not be the same. As it is a contiguous allocation, hence no spanning is allowed. Here partitions are made before execution or during system configure.
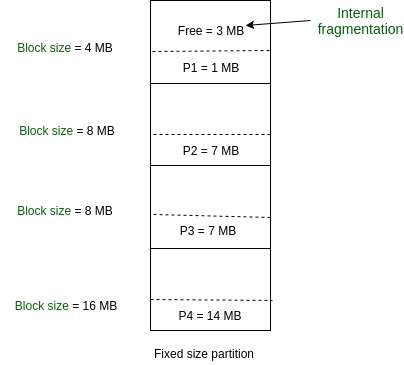
Disadvantages of Fixed Partitioning:
Internal Fragmentation:
External Fragmentation:
Limit process size:
Limitation on Degree of Multiprogramming:
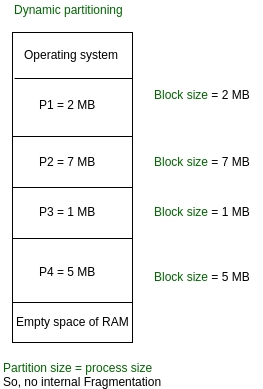
2. Variable Partitioning
It is a part of Contiguous allocation technique. It is used to alleviate the problem faced by Fixed Partitioning. In contrast with fixed partitioning, partitions are not made before the execution or during system configure. Various features associated with variable Partitioning-
Initially RAM is empty and partitions are made during the run-time according to process’s need instead of partitioning during system configure.
The size of partition will be equal to incoming process.
The partition size varies according to the need of the process so that the internal fragmentation can be avoided to ensure efficient utilisation of RAM.
Number of partitions in RAM is not fixed and depends on the number of incoming process and Main Memory’s size.
Advantages of Variable Partitioning –
No Internal Fragmentation
No restriction on Degree of Multiprogramming:
No Limitation on the size of the process:
Disadvantages of Variable Partitioning –
Difficult Implementation:
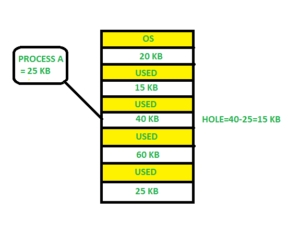
External Fragmentation: There will be external fragmentation in spite of absence of internal fragmentation.
For example, suppose in above example- process P1(2MB) and process P3(1MB) completed their execution.
Partition Allocation
In Partition Allocation, when there is more than one partition freely available to accommodate a process’s request, a partition must be selected. To choose a particular partition, a partition allocation method is needed. There are different Placement Algorithm: A. First Fit B. Best Fit C. Worst Fit D. Next Fit
1. First Fit: In the first fit, the partition is allocated which is the first sufficient block from the top of Main Memory. It scans memory from the beginning and chooses the first available block that is large enough. Thus it allocates the first hole that is large enough.
2. Best Fit Allocate the process to the partition which is the first smallest sufficient partition among the free available partition. It searches the entire list of holes to find the smallest hole whose size is greater than or equal to the size of the process.
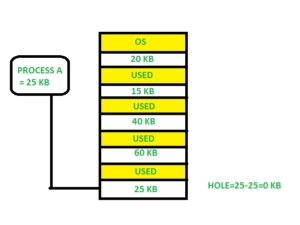
3. Worst Fit Allocate the process to the partition which is the largest sufficient among the freely available partitions available in the main memory. It is opposite to the best-fit algorithm. It searches the entire list of holes to find the largest hole and allocate it to process.
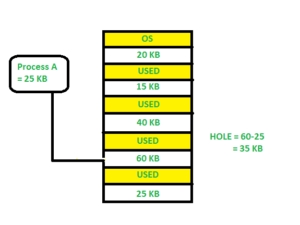
4. Next Fit: Next fit is similar to the first fit but it will search for the first sufficient partition from the last allocation point.
Non-Contiguous Allocation
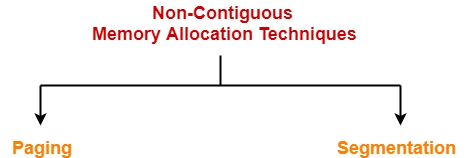
Paging
Logical Address space:
An address generated by the CPU is known as “Logical Address”. It is also known as a Virtual address. Logical address space can be defined as the size of the process.
Physical Address space:
An address seen by the memory unit (i.e the one loaded into the memory address register of the memory) is commonly known as a “Physical Address”.
Paging is a memory management scheme that eliminates the need for contiguous allocation
This scheme permits the physical address space of a process to be non – contiguous.
The mapping from virtual to physical address is done by the memory management unit (MMU) which is a hardware device and this mapping is known as paging technique.
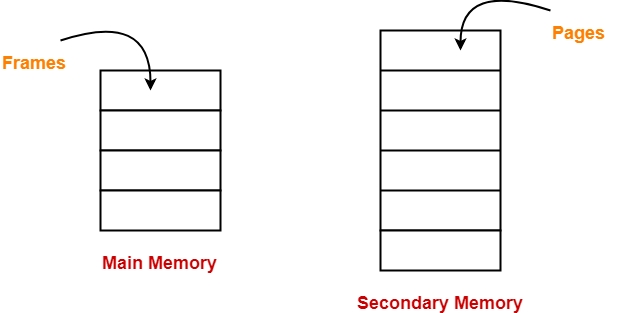
The Physical Address Space is conceptually divided into a number of fixed-size blocks, called frames.
The Logical address Space is also splitted into fixed-size blocks, called pages.
Page Size = Frame Size
The partitions of secondary memory are called as pages.
The partitions of main memory are called as frames.
Consider a process is divided into 4 pages P0, P1, P2 and P3.
Depending upon the availability, these pages may be stored in the main memory frames in a non-contiguous fashion as shown-

Translating Logical Address into Physical Address-
CPU always generates a logical address.
A physical address is needed to access the main memory.
Following steps are followed to translate logical address into physical address-
Step-01:
CPU generates a logical address consisting of two parts-
Page Number
Page Offset
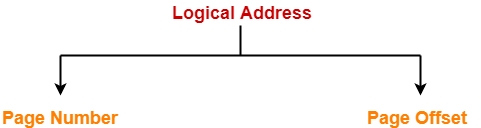
Page Number specifies the specific page of the process from which CPU wants to read the data.
Page Offset specifies the specific word on the page that CPU wants to read.
Step-02:
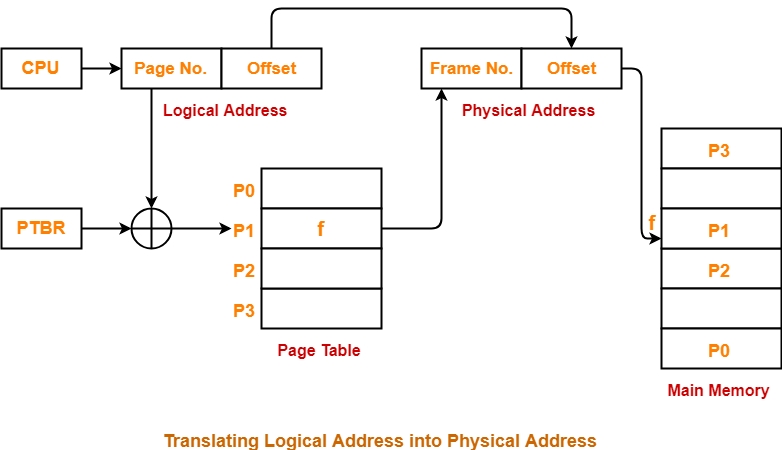
For the page number generated by the CPU,
Page Table provides the corresponding frame number (base address of the frame) where that page is stored in the main memory.
Step-03:
The frame number combined with the page offset forms the required physical address.
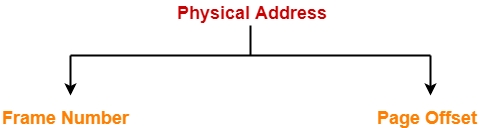
Frame number specifies the specific frame where the required page is stored.
Page Offset specifies the specific word that has to be read from that page.
Diagram-
The following diagram illustrates the above steps of translating logical address into physical address-
Advantages:-
It allows to store parts of a single process in a non-contiguous fashion. It solves the problem of external fragmentation.
Disadvantages:-
There is an overhead of maintaining a page table for each process.
Segmentation
Like Paging, Segmentation is another non-contiguous memory allocation technique.
In segmentation, process is not divided blindly into fixed size pages.
Rather, the process is divided into modules for better visualization.
Characteristics:-
Segmentation is a variable size partitioning scheme.
In segmentation, secondary memory and main memory are divided into partitions of unequal size.
The size of partitions depend on the length of modules.
The partitions of secondary memory are called as segments.
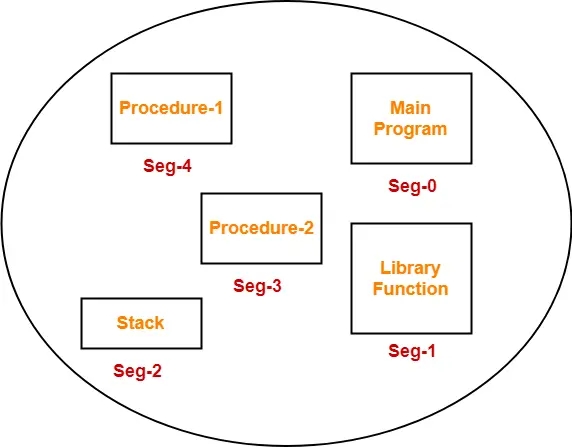
Example-
Consider a program is divided into 5 segments as-
Segment Table
Segment table is a table that stores the information about each segment of the process.
It has two columns.
First column stores the size or length of the segment.
Second column stores the base address or starting address of the segment in the main memory.
Segment table is stored as a separate segment in the main memory.
Segment table base register (STBR) stores the base address of the segment table.
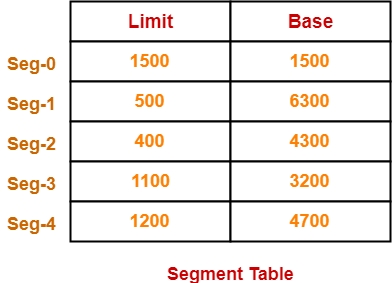
For the above illustration, consider the segment table is-
Here,
Limit indicates the length or size of the segment.
Base indicates the base address or starting address of the segment in the main memory.
In accordance to the above segment table, the segments are stored in the main memory as-

Translating Logical Address into Physical Address-
CPU always generates a logical address.
A physical address is needed to access the main memory.
Following steps are followed to translate logical address into physical address-
Step-01:
CPU generates a logical address consisting of two parts-
Segment Number
Segment Offset
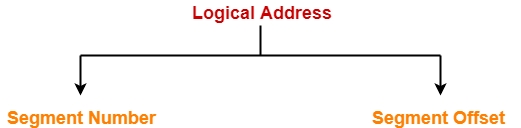
Segment Number specifies the specific segment of the process from which CPU wants to read the data.
Segment Offset specifies the specific word in the segment that CPU wants to read.
Step-02:
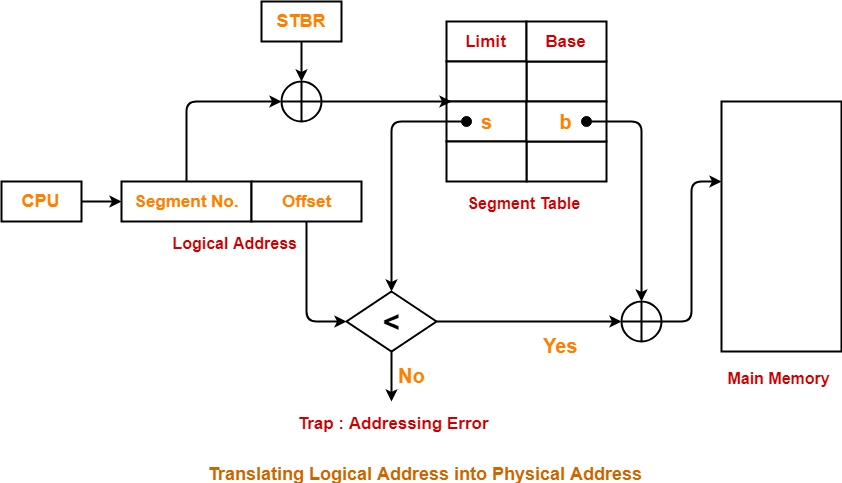
For the generated segment number, corresponding entry is located in the segment table.
Then, segment offset is compared with the limit (size) of the segment.
Now, two cases are possible-
Case-01: Segment Offset >= Limit
If segment offset is found to be greater than or equal to the limit, a trap is generated.
Case-02: Segment Offset < Limit
If segment offset is found to be smaller than the limit, then request is treated as a valid request.
The segment offset must always lie in the range [0, limit-1],
Then, segment offset is added with the base address of the segment.
The result obtained after addition is the address of the memory location storing the required word.
Diagram-
The following diagram illustrates the above steps of translating logical address into physical address-
Advantages-
It allows to divide the program into modules which provides better visualization.
Segment table consumes less space as compared to Page Table in paging.
It solves the problem of internal fragmentation.
Disadvantages-
There is an overhead of maintaining a segment table for each process.
Overlays in Memory Management
The main problem in Fixed partitioning is the size of a process has to be limited by the maximum size of the partition, which means a process can never be span over another.In order to solve this problem, earlier people have used some solution which is called as Overlays.
The concept of overlays is that whenever a process is running it will not use the complete program at the same time, it will use only some part of it. Then overlays concept says that whatever part you required, you load it an once the part is done, then you just unload it, means just pull it back and get the new part you required and run it.
Swapping in Memory Management
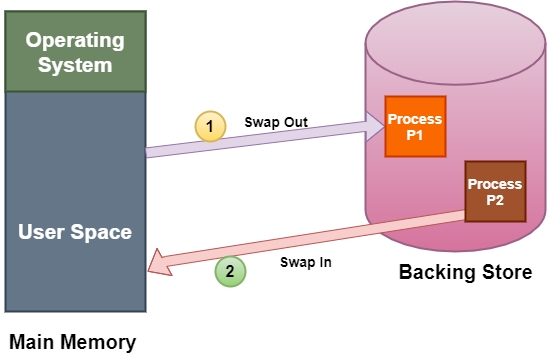
Swapping is a memory management scheme in which any process can be temporarily swapped from main memory to secondary memory so that the main memory can be made available for other processes.
Any process must be in the memory for its execution, but can be swapped temporarily out of memory to a backing store and then again brought back into the memory to complete its execution.Swapping is done so that other processes get memory for their execution. A variant of the swapping technique is the priority-based scheduling algorithm
Advantages of Swapping
The advantages/benefits of the Swapping technique are as follows:
The swapping technique mainly helps the CPU to manage multiple processes within a single main memory.
This technique helps to create and use virtual memory.
With the help of this technique, the CPU can perform several tasks simultaneously. Thus, processes need not wait too long before their execution.
Virtual Memory
Virtual Memory mainly gives the illusion of more physical memory than there really is.
Virtual Memory is a space where large programs can store themselves in form of pages while their execution and only the required pages or portions of processes are loaded into the main memory. This technique is useful as a large virtual memory is provided for user programs when a very small physical memory is there. Thus Virtual memory is a technique that allows the execution of processes that are not in the physical memory completely.
Page Fault in OS
Page fault dominates more like an error. It mainly occurs when any program tries to access the data or the code that is in the address space of the program, but that data is not currently located in the RAM of the system.
So basically when the page referenced by the CPU is not found in the main memory then the situation is termed as Page Fault.
Whenever any page fault occurs, then the required page has to be fetched from the secondary memory into the main memory.
In case if the required page is not loaded into the memory, then a page fault trap arises.
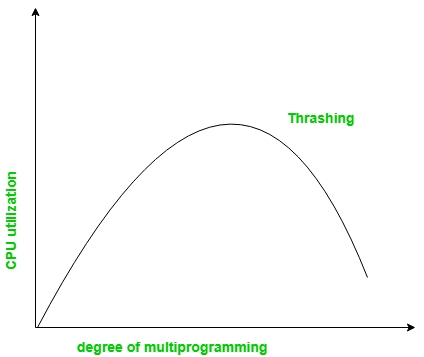
Thrashing in Operating System
Thrashing is a condition or a situation when the system is spending a major portion of its time in servicing the page faults, but the actual processing done is very negligible.
The basic concept involved is that if a process is allocated too few frames, then there will be too many and too frequent page faults. As a result, no useful work would be done by the CPU and the CPU utilisation would fall drastically. The long-term scheduler would then try to improve the CPU utilisation by loading some more processes into the memory thereby increasing the degree of multiprogramming. This would result in a further decrease in the CPU utilization triggering a chained reaction of higher page faults followed by an increase in the degree of multiprogramming, called Thrashing.
Page Replacement Algorithms
Last updated