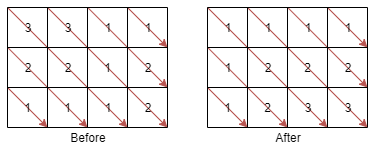
30. Sort the Matrix Diagonally

A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].

Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.

Example 1:

Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]

Example 2:

Input: mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
Output: [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]

Solution:

Approach Using index(i-j) as the key and storing all diagonal elements Sorting all diagonal Coping values to original matrix

class Solution
{
public:
    vector<vector<int>> diagonalSort(vector<vector<int>> &mat)
    {

        int n = mat.size();
        int m = mat[0].size();

        unordered_map<int, vector<int>> mp;

        for (int i = 0; i < n; i++)
        {

            for (int j = 0; j < m; j++)
            {
                mp[i - j].push_back(mat[i][j]);
            }
        }

        for (auto itr = mp.begin(); itr != mp.end(); itr++)
        {
            sort(itr->second.begin(), itr->second.end());
        }

        for (int i = n - 1; i >= 0; i--)
        {
            for (int j = m - 1; j >= 0; j--)
            {
                int idx = i - j;
                mat[i][j] = mp[idx].back();
                mp[idx].pop_back();
            }
        }

        return mat;
    }
};

Time Complexity: O(n *m * dlogd ) d=min(n,m)