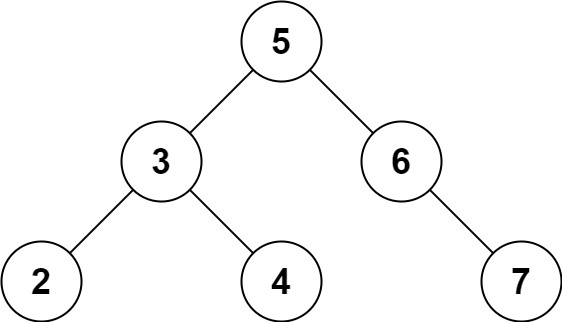
11.Two Sum IV - Input is a BST

Given the root of a Binary Search Tree and a target number k, return true if there exist two elements in the BST such that their sum is equal to the given target.

Example 1:

Input: root = [5,3,6,2,4,null,7], k = 9
Output: true

Example 2:

Input: root = [5,3,6,2,4,null,7], k = 28
Output: false

Solution: (BFS + SET)

class Solution
{
public:
    bool findTarget(TreeNode *root, int k)
    {

        unordered_set<int> s;

        queue<TreeNode *> q;

        q.push(root);

        while (!q.empty())
        {

            TreeNode *t = q.front();
            q.pop();

            int x = t->val;
            if (s.find(k - x) != s.end())
            {
                return true;
            }

            s.insert(x);

            if (t->left)
            {
                q.push(t->left);
            }

            if (t->right)
            {
                q.push(t->right);
            }
        }

        return false;
    }
};

Complexity Analysis

• Time complexity : O(n). We need to traverse over the whole tree once in the worst case. Here, n refers to the number of nodes in the given tree.

• Space complexity : O(n). The size of the set can grow atmost upto n.

Solution: (Using BST)

Doing preorder traversal to get an array of sorted order Then Two Sum in a sorted array

class Solution
{
public:
    bool findTarget(TreeNode *root, int k)
    {

        stack<TreeNode *> s;
        TreeNode *t = root;
        vector<int> v;
        while (t != NULL || !s.empty())
        {

            if (t != NULL)
            {
                s.push(t);
                t = t->left;
            }
            else
            {
                t = s.top();
                v.push_back(t->val);
                s.pop();
                t = t->right;
            }
        }

        int start = 0;
        int end = v.size() - 1;

        while (start < end)
        {

            if ((v[start] + v[end] - k) == 0)
            {
                return true;
            }
            else if (k - (v[start] + v[end]) < 0)
            {
                end--;
            }
            else
            {
                start++;
            }
        }

        return false;
    }
};

• Time complexity : O(n). We need to traverse over the whole tree once to do the inorder traversal. Here, n refers to the number of nodes in the given tree.

• Space complexity : O(n). The sorted listlist will contain n elements.