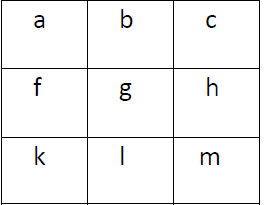
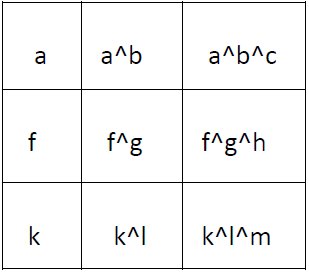
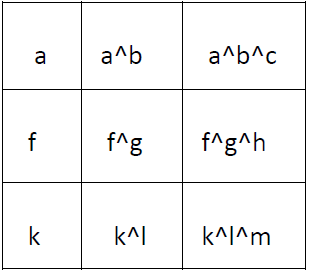
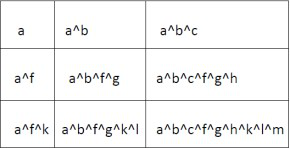
5. Find Kth Largest XOR Coordinate Value

You are given a 2D matrix of size m x n, consisting of non-negative integers. You are also given an integer k.

The value of coordinate (a, b) of the matrix is the XOR of all matrix[i][j] where 0 <= i <= a < m and 0 <= j <= b < n (0-indexed).

Find the kth largest value (1-indexed) of all the coordinates of matrix.

Example 1:
Input: matrix = [[5,2],[1,6]], k = 1
Output: 7
Explanation: The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.

Example 2:
Input: matrix = [[5,2],[1,6]], k = 2
Output: 5
Explanation: The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.

Example 3:
Input: matrix = [[5,2],[1,6]], k = 3
Output: 4
Explanation: The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.

Example 4:
Input: matrix = [[5,2],[1,6]], k = 4
Output: 0
Explanation: The value of coordinate (1,1) is 5 XOR 2 XOR 1 XOR 6 = 0, which is the 4th largest value.

Solution:

Approach: Step 1: Change the matrix so that matrix[i][j] will contain the xor of all the numbers in the ith row upto jth column as shown below.

---------->

Step 2: Change the above created matrix so that matrix[i][j] will contain the xor of all the numbers in the jth column upto ith row as shown below.

----->

class Solution
{
public:
    int kthLargestValue(vector<vector<int>> &matrix, int k)
    {

        int n = matrix.size();
        int m = matrix[0].size();

        vector<vector<int>> v(n, vector<int>(m, 0));
        priority_queue<int> pq;

        for (int i = 0; i < matrix.size(); i++)
        {
            for (int j = 0; j < matrix[0].size(); j++)
            {
                if (j == 0)
                {
                    v[i][j] = matrix[i][j];
                }
                else
                {
                    v[i][j] = v[i][j - 1] ^ matrix[i][j];
                }
            }
        }

        for (int i = 0; i < matrix.size(); i++)
        {
            for (int j = 0; j < matrix[0].size(); j++)
            {
                if (i == 0)
                {
                    continue;
                }

                v[i][j] = v[i - 1][j] ^ v[i][j];
            }
        }

        for (int i = 0; i < v.size(); i++)
        {
            for (int j = 0; j < v[0].size(); j++)
            {
             
                pq.push(v[i][j]);
            }
        }

        for (int i = 1; i < k; i++)
        {
            pq.pop();
        }

        return pq.top();
    }
};

Time Complexity : O(NM logK)