Quick Sort

Algorithm

/* low  --> Starting index,  high  --> Ending index */

quickSort(arr[], low, high)
{
    if (low < high)
    {
        /* pi is partitioning index, arr[pi] is now
           at right place */
        pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1);  // Before pi
        quickSort(arr, pi + 1, high); // After pi
    }
}

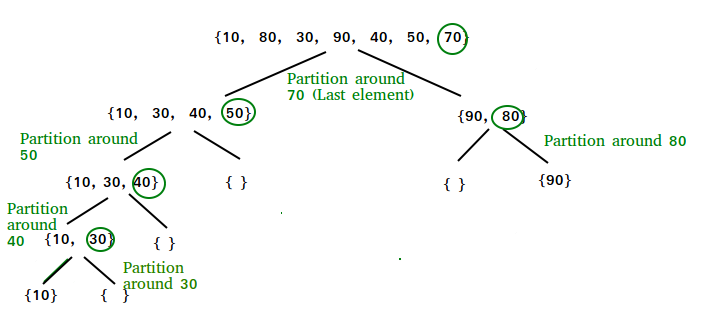
/* This function takes last element as pivot, places
   the pivot element at its correct position in sorted
    array, and places all smaller (smaller than pivot)
   to left of pivot and all greater elements to right
   of pivot */
   
partition (arr[], low, high)
{
    // pivot (Element to be placed at right position)
    pivot = arr[high];  
 
    i = (low - 1)  // Index of smaller element

    for (j = low; j <= high- 1; j++)
    {
        // If current element is smaller than the pivot
        if (arr[j] < pivot)
        {
            i++;    // increment index of smaller element
            swap arr[i] and arr[j]
        }
    }
    swap arr[i + 1] and arr[high])
    return (i + 1)
}

quicksort

Code

class Solution
{
public:
    int getPivot(vector<int> &nums, int start, int end)
    {

        int pvt = nums[end];
        int k = start;

        for (int i = start; i <= end - 1; i++)
        {
            if (nums[i] < pvt)
            {
                swap(nums[k], nums[i]);
                k++;
            }
        }
        swap(nums[k], nums[end]);
        return k;
    }
    
    void quickSort(vector<int> &nums, int start, int end)
    {

        if (start >= end)
        {
            return;
        }
        int pvt = getPivot(nums, start, end);
        quickSort(nums, start, pvt - 1);
        quickSort(nums, pvt + 1, end);

        return;
    }
    
    vector<int> sortArray(vector<int> &nums)
    {

        int n = nums.size();
        quickSort(nums, 0, n - 1);

        return nums;
    }
};

Analysis of QuickSort Worst Case: O(n2).

Best Case: O(nLogn).

Average Case: O(nLogn)