31. Minimum Falling Path Sum

Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix

A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).

Example 1:

Input: matrix = [[2,1,3],[6,5,4],[7,8,9]]
Output: 13
Explanation: There are two falling paths with a minimum sum underlined below:
[[2,1,3],      [[2,1,3],
 [6,5,4],       [6,5,4],
 [7,8,9]]       [7,8,9]]

Example 2:

Input: matrix = [[-19,57],[-40,-5]]
Output: -59
Explanation: The falling path with a minimum sum is underlined below:
[[-19,57],
 [-40,-5]]

Example 3:

Input: matrix = [[-48]]
Output: -48

Solution: (DP)

Approach: In each case we have 3 choices we choose the minimum of all.

image

class Solution
{
public:
    int minFallingPathSum(vector<vector<int>> &matrix)
    {
        int n = matrix.size();
        vector<vector<int>> dp(n, vector<int>(n + 2, 200));

        for (int i = 0; i < n; i++)
        {
            for (int j = 1; j <= n; j++)
            {
                dp[i][j] = matrix[i][j - 1];
            }
        }

        for (int i = 1; i < n; i++)
        {
            for (int j = 1; j <= n; j++)
            {
                dp[i][j] = min(dp[i][j] + dp[i - 1][j], min(dp[i][j] + dp[i - 1][j - 1], dp[i][j] + dp[i - 1][j + 1]));
            }
        }

        int res = INT_MAX;
        for (int i = 1; i <= n; i++)
        {
            if (dp[n - 1][i] < res)
            {
                res = dp[n - 1][i];
            }
        }

        return res;
    }
};

Using an extra space

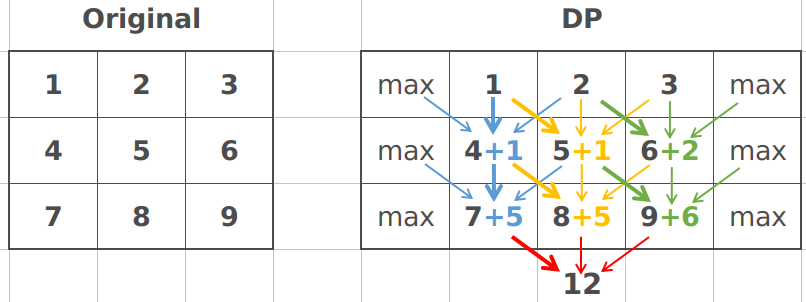
Solution: (Optimized DP)

class Solution
{
public:
    int minFallingPathSum(vector<vector<int>> &matrix)
    {

        int n = matrix.size();

        for (int i = 1; i < n; i++)
        {
            for (int j = 0; j < n; j++)
            {

                int left = (j - 1 >= 0) ? matrix[i - 1][j - 1] : 200;
                int right = (j + 1 < n) ? matrix[i - 1][j + 1] : 200;
                int top = matrix[i - 1][j];

                matrix[i][j] = min(matrix[i][j] + left, min(matrix[i][j] + top, matrix[i][j] + right));
            }
        }

        int res = INT_MAX;
        for (int i = 0; i < n; i++)
        {
            res = min(res, matrix[n - 1][i]);
        }

        return res;
    }
};

Using Constant extra space