16. Minimum Number of Taps to Open to Water a Garden

There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).

There are n + 1 taps located at points [0, 1, ..., n] in the garden.

Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.

Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

Example 1:

Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]

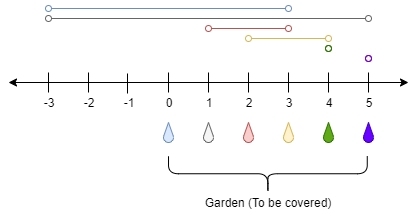
Example 2:

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.

Example 3:

Input: n = 7, ranges = [1,2,1,0,2,1,0,1]
Output: 3

Example 4:

Input: n = 8, ranges = [4,0,0,0,0,0,0,0,4]
Output: 2

Example 5:

Input: n = 8, ranges = [4,0,0,0,4,0,0,0,4]
Output: 1

Solution: (DP)

class Solution
{
public:
    int minTaps(int n, vector<int> &ranges)
    {

        vector<vector<int>> v;
        vector<int> dp(n + 1, n + 2);

        for (int i = 0; i < ranges.size(); i++)
        {
            int val = ranges[i];
            v.push_back({i - val, i + val});
        }

        sort(v.begin(), v.end());

        dp[0] = 0;

        for (int i = 0; i < v.size(); i++)
        {
            int start = max(0, v[i][0]);
            int end = min(n, v[i][1]);

            for (int j = start; j <= end; j++)
            {
                dp[j] = min(dp[j], dp[start] + 1);
            }
        }

        if (dp[n] == n + 2)
        {
            return -1;
        }

        return dp[n];
    }
};

Time Complexity: O(n * time)

Solution: (Greedy)

class Solution
{
public:
    int videoStitching(vector<vector<int>> &clips, int time)
    {

        sort(clips.begin(), clips.end());

        int maxEnd = 0;

        int count = 0;

        int i = 0;
        while (maxEnd < time)
        {
            int curEnd = 0;
            while (i < clips.size() && clips[i][0] <= maxEnd)
            {
                curEnd = max(curEnd, clips[i][1]);
                i++;
            }

            if (curEnd <= maxEnd)
            {
                return -1;
            }

            count++;
            maxEnd = curEnd;
        }

        return count;
    }
};