Concepts of Heap
A Heap is a special Tree-based data structure in which the tree is a complete binary tree.
Binary Heap
A Binary Heap is a Binary Tree with following properties. 1) It’s a complete tree (All levels are completely filled except possibly the last level and the last level has all keys as left as possible). This property of Binary Heap makes them suitable to be stored in an array.
2) A Binary Heap is either Min Heap or Max Heap.
Max-Heap: In a Max-Heap the key present at the root node must be greatest among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
Min-Heap: In a Min-Heap the key present at the root node must be minimum among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
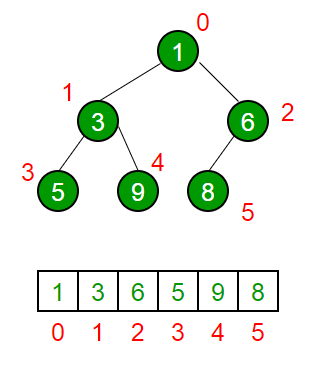
How is Binary Heap represented
A Binary Heap is a Complete Binary Tree. A binary heap is typically represented as an array.
The root element will be at Arr[0].
Below table shows indexes of other nodes for the ith node, i.e., Arr[i]:
Arr[(i-1)/2]
Returns the parent node
Arr[(2*i)+1]
Returns the left child node
Arr[(2*i)+2]
Returns the right child node
Applications of Heaps:
1) Heap Sort: Heap Sort uses Binary Heap to sort an array in O(nLogn) time.
2) Priority Queue: Priority queues can be efficiently implemented using Binary Heap because it supports insert(), delete() and extractmax(), decreaseKey() operations in O(logn) time.
Other Heaps
Heaps are mainly used for implementing priority queue.
Binomial Heap
Binomial Heap is an extension of Binary Heap that provides faster union or merge operation together with other operations provided by Binary Heap.
Fibonacci Heap
In terms of Time Complexity, Fibonacci Heap beats both Binary and Binomial Heaps. Like Binomial Heap, Fibonacci Heap is a collection of trees with min-heap or max-heap property.
Last updated
